Supongamos que nos interesa encontrar:
(1) la constante de normalización de
![]() en (2);
en (2);
(2) el valor esperado final de ![]() ; y
; y
(3) la densidad predictiva de ![]() .
.
En este caso resulta conveniente trabajar en términos de la
reparametrización
![]() . La densidad final de
. La densidad final de ![]() se
obtiene fácilmente de (2) a través de un cambio de variable,
y está dada por
se
obtiene fácilmente de (2) a través de un cambio de variable,
y está dada por
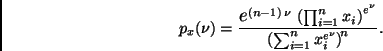
![]() Aproximación normal asintótica. Una primera
aproximación a
Aproximación normal asintótica. Una primera
aproximación a
![]() , que será de mucha utilidad en la
aplicación de algunos de los métodos discutidos más adelante, es
, que será de mucha utilidad en la
aplicación de algunos de los métodos discutidos más adelante, es
![]() Aproximación de Laplace para la constante de
normalización de
Aproximación de Laplace para la constante de
normalización de
![]() .
.
![]() Valor esperado final de
Valor esperado final de ![]() . De acuerdo con
el resultado del Ejemplo 2.1, la forma estándar de la aproximación
de Laplace está dada en este caso por
. De acuerdo con
el resultado del Ejemplo 2.1, la forma estándar de la aproximación
de Laplace está dada en este caso por
![]() Densidad predictiva de
Densidad predictiva de ![]() . Notemos primero que
la integral (3) puede escribirse como
. Notemos primero que
la integral (3) puede escribirse como
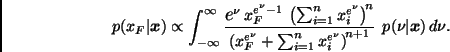
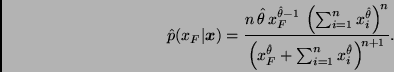
![[*]](crossref.png) muestra la gráfica
de esta aproximación a la densidad predictiva de
muestra la gráfica
de esta aproximación a la densidad predictiva de