

Next: 2 Forma exponencial
Up: 2 Aproximación de Laplace
Previous: 2 Aproximación de Laplace
Supongamos que se desea calcular una integral de la forma
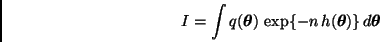 |
(5) |
donde
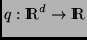 y
y
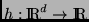 son
funciones suaves de
son
funciones suaves de
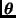 . Supongamos también que
. Supongamos también que 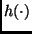 tiene un mínimo en
tiene un mínimo en
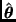 . El método de Laplace
aproxima
. El método de Laplace
aproxima 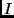 a través de
a través de
donde
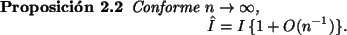

Notemos que, en general, una integral dada
puede escribirse como
para distintas funciones 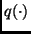 y
y 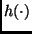 . Para un valor fijo de
. Para un valor fijo de 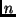 ,
la precisión de la aproximación de Laplace depende tanto de la elección
particular de estas funciones como de la parametrización que se utilice.
Por otra parte, es posible lograr una mayor precisión si se mantienen
algunos términos de orden mayor en la expansión en serie de Taylor, pero
esto requiere a su vez del cálculo de derivadas de orden mayor. En
ocasiones
,
la precisión de la aproximación de Laplace depende tanto de la elección
particular de estas funciones como de la parametrización que se utilice.
Por otra parte, es posible lograr una mayor precisión si se mantienen
algunos términos de orden mayor en la expansión en serie de Taylor, pero
esto requiere a su vez del cálculo de derivadas de orden mayor. En
ocasiones 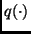 y
y 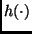 se eligen de manera que el valor de
se eligen de manera que el valor de
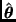 pueda encontrarse fácilmente (de preferencia en
forma analítica). De esta manera se obtiene una aproximación rápida
y simple, aunque no siempre suficientemente precisa. Al igual que en el caso
de la aproximación normal, en aplicaciones específicas generalmente
no es posible determinar de manera sencilla si la aproximación de Laplace
es adecuada para el tamaño de muestra dado.
pueda encontrarse fácilmente (de preferencia en
forma analítica). De esta manera se obtiene una aproximación rápida
y simple, aunque no siempre suficientemente precisa. Al igual que en el caso
de la aproximación normal, en aplicaciones específicas generalmente
no es posible determinar de manera sencilla si la aproximación de Laplace
es adecuada para el tamaño de muestra dado.



Next: 2 Forma exponencial
Up: 2 Aproximación de Laplace
Previous: 2 Aproximación de Laplace