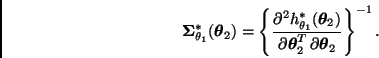

Next: 3 Ejemplo A
Up: 2 Aproximación de Laplace
Previous: 2 Forma exponencial
Sea
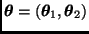 , con
, con
 y
y
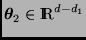 .
Supongamos que la distribución de
.
Supongamos que la distribución de
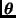 se escribe como
se escribe como
donde 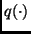 y
y 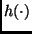 son funciones suaves, y que interesa calcular
la densidad marginal de
son funciones suaves, y que interesa calcular
la densidad marginal de
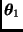 , i.e.
, i.e.
Para cada valor de
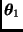 , sean
, sean
de manera que
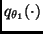 y
y
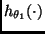 son,
respectivamente,
son,
respectivamente, 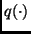 y
y 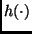 vistas sólo como funciones de
vistas sólo como funciones de
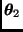 . Finalmente, supongamos que
. Finalmente, supongamos que
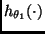 tiene
un mínimo en
tiene
un mínimo en
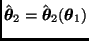 .
.
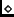 Forma estándar. La forma estándar de la
aproximación de Laplace se reduce entonces a
Forma estándar. La forma estándar de la
aproximación de Laplace se reduce entonces a
donde
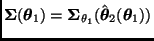 , con
, con
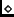 Forma exponencial. Notemos que la distribución
de
Forma exponencial. Notemos que la distribución
de
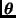 también puede escribirse como
también puede escribirse como
con
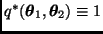 y
y
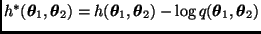 . Como antes, para cada valor de
. Como antes, para cada valor de
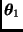 definimos
definimos
y suponemos que
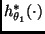 tiene un mínimo en
tiene un mínimo en
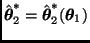 .
La forma exponencial de la aproximación de Laplace se reduce entonces a
.
La forma exponencial de la aproximación de Laplace se reduce entonces a
donde
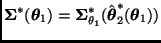 ,
con
,
con


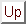

Next: 3 Ejemplo A
Up: 2 Aproximación de Laplace
Previous: 2 Forma exponencial
![]() , con
, con
![]() y
y
![]() .
Supongamos que la distribución de
.
Supongamos que la distribución de
![]() se escribe como
se escribe como
![]() , sean
, sean
![]() Forma estándar. La forma estándar de la
aproximación de Laplace se reduce entonces a
Forma estándar. La forma estándar de la
aproximación de Laplace se reduce entonces a
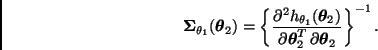
![]() Forma exponencial. Notemos que la distribución
de
Forma exponencial. Notemos que la distribución
de
![]() también puede escribirse como
también puede escribirse como