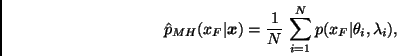Para ilustrar el uso del algoritmo de Metropolis-Hastings
(independencia), supongamos que nos interesa obtener una muestra de
tamaño ![]() de
de
![]() . Como antes, resulta
conveniente trabajar en términos de
. Como antes, resulta
conveniente trabajar en términos de
![]() . En este caso
podemos utilizar la aproximación normal asintótica
. En este caso
podemos utilizar la aproximación normal asintótica
![]() como distribución de transición.
como distribución de transición.
Se decidió correr el algoritmo durante 1100 iteraciones, de las
cuales se tomaron las primeras 100 como periodo de calentamiento.
La Figura 1 muestra los promedios ergódicos de las
medias muestrales para algunas funciones de ![]() . La muestra
resultante puede transformarse fácilmente en una muestra de la
distribución final de
. La muestra
resultante puede transformarse fácilmente en una muestra de la
distribución final de ![]() a través de la relación
a través de la relación
![]() . En la Figura 2 se presenta el
histograma correspondiente junto con una estimación de la
función de densidad
. En la Figura 2 se presenta el
histograma correspondiente junto con una estimación de la
función de densidad
![]() .
.
Por otra parte, notemos que
Finalmente, es posible estimar la densidad predictiva de ![]() evaluando,
para cada valor de
evaluando,
para cada valor de ![]() ,
,