3 Ejemplo

Gelfand, Hills, Racine-Poon y Smith (1990) discuten el análisis Bayesiano de los datos presentados en la Tabla 2.

Estos datos corresponden a los pesos (en gramos) de 30 ratas jóvenes en un grupo de controles. El peso de cada una de las ratas fue medido a los $x_1=8$, $x_2=15$, $x_3=22$, $x_4=29$ y $x_5=36$ días de edad.

De acuerdo con Gelfand, Hills, Racine-Poon y Smith (1990), dado el periodo de tiempo considerado es razonable suponer un crecimiento lineal del peso de cada una de las ratas. Para simplificar el análisis, estos autores también suponen homoscedasticidad. Específicamente proponen el siguiente modelo jerárquico.

Nivel I.

$$Y_{ij} \sim N(\beta_{1i} + \beta_{2i} x_{ij}, \sigma^2)$$

donde $Y_{ij}$ y $x_{ij}$ denotan el peso y la edad, respectivamente, de la $i$-ésima rata al realizarse la $j$-ésima medición ($i=1,\ldots,30$; $j=1,\ldots,5$).

Nivel II.

$$\bmath{\beta}_i \sim N_2(\bmath{\alpha}, \bmath{\Sigma}_{\beta *}),$$

donde $\bmath{\beta}_i = (\beta_{1i}, \beta_{2i})'$; $i=1,\ldots,30$.

Nivel III.

$$\bmath{\alpha} \sim N_2(\bmath{\alpha}_0, \bmath{\Sigma}_\alpha),$$

Table 2: Crecimiento de un grupo de ratas (controles)

Rata	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	Rata	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$
1	151	199	246	283	320	16	160	207	248	288	324
2	145	199	249	293	354	17	142	187	234	280	316
3	147	214	263	312	328	18	156	203	243	283	317
4	155	200	237	272	297	19	157	212	259	307	336
5	135	188	230	280	323	20	152	203	246	286	321
6	159	210	252	298	331	21	154	205	253	298	334
7	141	189	231	275	305	22	139	190	225	267	302
8	159	201	248	297	338	23	146	191	229	272	302
9	177	236	285	340	376	24	157	211	250	285	323
10	134	182	220	260	296	25	132	185	237	286	331
11	160	208	261	313	352	26	160	207	257	303	345
12	143	188	220	273	314	27	169	216	261	295	333
13	154	200	244	289	325	28	157	205	248	289	316
14	171	221	270	326	358	29	137	180	219	258	291
15	163	216	242	281	312	30	153	200	244	286	324

Gelfand, Hills, Racine-Poon y Smith (1990) consideran el caso en el que $\sigma^2$ y $\bmath{\Sigma}_{\beta *}$ son desconocidos y asignan una distribución inicial no informativa a estos parámetros. El análisis que presentan es exacto y se basa en el uso de una técnica de simulación conocida como Muestreo de Gibbs (ver, por ejemplo, Gilks, Richardson y Spiegelhalter, 1996).

Con el propósito de ilustrar el análisis aproximado discutido en la Sección 4.1.2, aquí analizaremos los datos de la Tabla 2 utilizando el modelo descrito en el Ejemplo 4.2. Para ello es necesario estimar primero los parámetros $\sigma^2$ y $\bmath{\Sigma}_{\beta *}$.

Sea $\hat{\bmath{\beta}}_i$ el estimador de mínimos cuadrados de $\bmath{\beta}_i$, basado exclusivamente en los datos de la $i$-ésima rata ($i=1,\ldots,30$), y sea

$$\hat{\bmath{\Sigma}}_{\beta *} = \frac{1}{30} \sum_{i=1}^{30... ...\beta}}^*) (\hat{\bmath{\beta}}_i - \hat{\bmath{\beta}}^*)',$$

donde

$$\hat{\bmath{\beta}}^* = \frac{1}{30} \sum_{i=1}^{30} \hat{\bmath{\beta}}_i$$

denota la ``media muestral'' de los estimadores $\hat{\bmath{\beta}}_i$. Por otro lado, sea

$$\hat{\sigma}^2 = \frac{1}{150} \sum_{i=1}^{30} \sum_{j=1}^{5} (y_{ij} - \hat{y}_{ij})^2,$$

donde $\hat{y}_{ij} = \hat{\beta}_{1i} + \hat{\beta}_{2i} x_{ij}$. En particular, para los datos de la Tabla 2 se tiene que $\hat{\sigma}^2 = 27.13$ y

$$\hat{\bmath{\Sigma}}_{\beta *} = \left( \begin{array}{cc} 158.39 & -2.50 \\ -2.50 & 0.33 \end{array}\right).$$

Figure 4: Distribución final para los coeficientes de la población y de la Rata 15

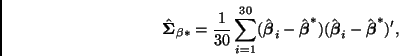
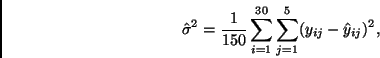
Para completar la especificación del modelo es necesario asignar una distribución inicial a $\bmath{\alpha}$. Aquí utilizaremos los valores $\bmath{\alpha}_0 = \mbmath{0}$ y

$$\bmath{\Sigma}_{\alpha} = \left( \begin{array}{cc} 10000 & 0 \\ 0 & 10000 \end{array}\right),$$

que corresponden a un estado de información inicial `vaga', pero que dan lugar a una distribución inicial propia para $\bmath{\alpha}$.

En la Figura 4 se presentan las distribuciones finales tanto para los coeficientes poblacionales como para los coeficientes correspondientes a la Rata 15: (a) $\beta_1$; (b) $\beta_2$; (c) $\beta_{1,15}$; (d) $\beta_{2,15}$. En términos generales, las inferencias sobre los coeficientes poblacionales $\beta_1$ y $\beta_2$ obtenidas a partir del presente análisis serán muy similares a las presentadas por Gelfand, Hills, Racine-Poon y Smith (1990; Figura 5). Debe señalarse, sin embargo, que nuestro análisis es aproximado y no toma en cuenta la incertidumbre sobre los valores de los parámetros $\sigma^2$ y $\bmath{\Sigma}_{\beta *}$, lo que podría llevar a sobreestimar la precisión de las inferencias sobre algunos de los parámetros restantes.

La Figura 5 muestra la distribución predictiva final para el peso de la Rata 15 a los 43 días de edad. El correspondiente intervalo de máxima densidad del 95% es (341.14, 369.71).

Figure 5: Distribución predictiva final del peso de la Rata 15 a los 43 días de edad