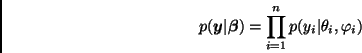
La clase de modelos presentada en la sección anterior puede extenderse para incluir modelos lineales generalizados en uno o varios de los niveles de la jerarquía. A manera de ilustración, consideremos el siguiente modelo:
Nivel I. (Observaciones)
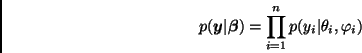
En otras palabras, las observaciones siguen una distribución en una familia exponencial. Por ejemplo, los modelos logísticos y loglineales corresponden a las familias Binomial y Poisson, respectivamente.
Nivel II. (Parámetros)
Nivel III. (Hiperparámetros)
El uso de distribuciones Normales en los niveles II y III resulta conveniente desde el punto de vista computacional, además de que generalmente pueden asignarse e interpretarse más fácilmente. Sin embargo, si estas especificaciones no describen adecuadamente la información inicial disponible, en principio es posible utilizar en su lugar las distribuciones conjugadas correspondientes, o cualquier otra familia que se considere apropiada.
En este caso la distribución final de ![]() y
y
![]() no puede
encontrarse analíticamente, aunque el modelo puede ser analizado a través
de métodos de simulación tales como Monte Carlo vía cadenas de Markov.
Por otra parte, un análisis aproximado y relativamente fácil de instrumentar es
posible si la aproximación Normal asintótica a la distribución final de
no puede
encontrarse analíticamente, aunque el modelo puede ser analizado a través
de métodos de simulación tales como Monte Carlo vía cadenas de Markov.
Por otra parte, un análisis aproximado y relativamente fácil de instrumentar es
posible si la aproximación Normal asintótica a la distribución final de
![]() y
y
![]() resulta adecuada en nuestra aplicación
particular (ver, por ejemplo, O'Hagan, 1994).
resulta adecuada en nuestra aplicación
particular (ver, por ejemplo, O'Hagan, 1994).
Otra posible extensión de los modelos jerárquicos discutidos en este trabajo consiste en incluir modelos no lineales en uno o más de los niveles de la jerarquía. El lector interesado puede consultar, por ejemplo, el trabajo de Bennet, Racine-Poon y Wakefield (1996).
Los modelos jerárquicos ofrecen una herramienta flexible y útil para modelar una gran variedad de situaciones que ocurren frecuentemente en la práctica, incluyendo el análisis de datos longitudinales y de muestreos estratificados así como problemas de meta-análisis.