El problema básico al analizar un modelo jerárquico es que la
distribución inicial de los parámetros no está completamente
especificada, sino que depende de un hiperparámetro que a su vez tiene
una distribución inicial propia. En otras palabras, el problema consiste
en hacer inferencias sobre las características individuales
![]() , así como sobre la
característica poblacional
, así como sobre la
característica poblacional ![]() . La distribución inicial
apropiada es entonces
. La distribución inicial
apropiada es entonces
La distribución final correspondiente es
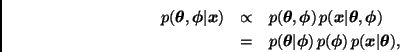
Por otra parte, la distribución marginal final de los parámetros está
dada por
Las inferencias acerca de ![]() y
y
![]() deben de basarse
en (8) y (9), respectivamente.
deben de basarse
en (8) y (9), respectivamente.
En general no es posible calcular estas distribuciones de manera analítica. Afortunadamente, existen técnicas de simulación que permiten analizar este tipo de modelos incluso en casos donde el número de parámetros es relativamente grande. Específicamente, los métodos de Monte Carlo vía cadenas de Markov (ver, por ejemplo, Gilks, Richardson y Spiegelhalter, 1996) han demostrado ser muy útiles en el análisis de los modelos jerárquicos.
Bajo ciertas condiciones, es posible realizar un análisis aproximado
relativamente sencillo. Si
![]() está
razonablemente concentrada alrededor de su moda,
está
razonablemente concentrada alrededor de su moda,
![]() ,
entonces
,
entonces
En otras palabras, es como si utilizáramos los datos para estimar
el valor de ![]() y entonces aplicáramos el Teorema de Bayes de la
manera usual en los dos primeros niveles de la jerarquía, tomando
y entonces aplicáramos el Teorema de Bayes de la
manera usual en los dos primeros niveles de la jerarquía, tomando
![]() . Este tipo de aproximaciones da lugar a
lo que comúnmente se conoce como Métodos Empíricos
Bayesianos. Un problema de estos métodos es que en general no toman en
cuenta la incertidumbre acerca de
. Este tipo de aproximaciones da lugar a
lo que comúnmente se conoce como Métodos Empíricos
Bayesianos. Un problema de estos métodos es que en general no toman en
cuenta la incertidumbre acerca de ![]() . El lector interesado puede
consultar el libro de Carlin y Louis (1996).
. El lector interesado puede
consultar el libro de Carlin y Louis (1996).
Predicción
Un modelo jerárquico está caracterizado por los parámetros
![]() y el hiperparámetro
y el hiperparámetro
![]() . En general, hay dos distribuciones predictivas que
podrían ser de interés:
(i) la distribución de una observación futura
. En general, hay dos distribuciones predictivas que
podrían ser de interés:
(i) la distribución de una observación futura ![]() correspondiente a uno de los parámetros
correspondiente a uno de los parámetros
![]() existentes;
y
(ii) la distribución de una observación
existentes;
y
(ii) la distribución de una observación ![]() correspondiente a una futura
correspondiente a una futura
![]() que proviene de la misma
población que dio lugar a los parámetros
que proviene de la misma
población que dio lugar a los parámetros
![]() .
.
Como en el caso de la distribución final, en general estas distribuciones predictivas no pueden encontrarse analíticamente pero pueden ser analizadas a través de métodos de simulación.
A continuación discutiremos con cierto detalle un modelo particular ampliamente utilizado en la práctica y que puede analizarse sin necesidad de métodos numéricos sofisticados.