1 Intercambiabilidad

Consideremos una serie de experimentos $\{ E_i: i=1,\ldots,k\}$, donde $E_i$ produce observaciones $\bmath{x}_i$ cuya distribución depende del parámetro $\bmath{\theta}_i$. De esta manera, cada $E_i$ tiene asociada una función de verosimilitud $p(\bmath{x}_i\vert\bmath{\theta}_i)$. (Cabe mencionar que los métodos descritos en esta sección son también aplicables a datos observacionales que tengan una estructura jerárquica.)

Comentario. Algunos de los parámetros pueden ser comunes a todos los experimentos. Por ejemplo, cada vector $\bmath{x}_i$ puede ser una muestra de observaciones de una distribución Normal con media $\mu_i$ y varianza común $\sigma^2$, de manera que $\bmath{\theta}_i=(\mu_i,\sigma^2)$.

Si no contamos con información que nos permita distinguir cualquiera de los parámetros $\bmath{\theta}_i$ de los otros (aparte de las observaciones $\bmath{x}_i$), y si no es razonable establecer algún orden o agrupamiento de los parámetros, entonces debemos suponer alguna forma de simetría entre éstos. Dicha simetría debe verse reflejada en la distribución inicial de los parámetros $\bmath{\theta}_i$ y se representa probabilísticamente a través del concepto de intercambiabilidad discutido en la Sección 2.2. De esta manera,

$$p(\bmath{\theta}_1,\ldots,\bmath{\theta}_k) = \int \left\{ ... ...h{\theta}_i\vert\bmath{\phi}) \right\} \, dQ_0(\bmath{\phi}).$$

Por otro lado, a nivel de las observaciones se tiene

$$\begin{eqnarray*} p(\bmath{x}_1,\ldots,\bmath{x}_k) & = & \int \left\{ \prod_{i... ...a}_i) \right\} \, dQ(\bmath{\theta}_1,\ldots,\bmath{\theta}_k), \end{eqnarray*}$$

donde $dQ(\bmath{\theta}_1,\ldots,\bmath{\theta}_k) = p(\bmath{\theta}_1,\ldots,\bmath{\theta}_k) \, d\bmath{\theta}_1 \cdots d\bmath{\theta}_k$. La forma de estas distribuciones como mezclas de distribuciones de observaciones independientes e idénticamente distribuidas, es generalmente todo lo que se necesita en la práctica para capturar la idea de intercambiabilidad.

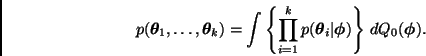
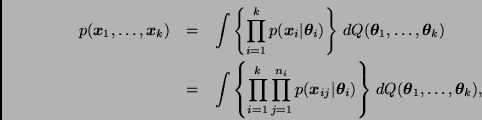
A manera de resumen, podemos decir que un modelo jerárquico tiene la siguiente estructura:

Nivel I. (Observaciones)

$$\begin{eqnarray*} p(\bmath{x}\vert\bmath{\theta}) & = & p(\bmath{x}_1,\ldots,\bm... ... \\ & = & \prod_{i=1}^{k} p(\bmath{x}_i\vert\bmath{\theta}_i). \end{eqnarray*}$$

Nivel II. (Parámetros)

$$\begin{eqnarray*} p(\bmath{\theta}\vert\bmath{\phi}) & = & p(\bmath{\theta}_1,\l... ...\\ & = & \prod_{i=1}^{k} p(\bmath{\theta}_i\vert\bmath{\phi}). \end{eqnarray*}$$

Nivel III. (Hiperparámetros)

$$p(\bmath{\phi})$$

Este modelo puede interpretarse de la siguiente manera:

• Las observaciones $\bmath{x}_1,\ldots,\bmath{x}_k$ provienen de experimentos distintos pero de alguna forma relacionados entre sí (experimentos realizados en $k$ centros de investigación involucrados en el mismo estudio sobre una afección renal).

• Los parámetros $\bmath{\theta}_1,\ldots,\bmath{\theta}_k$ se suponen intercambiables, en vista de la posible relación entre las $k$ muestras observadas ($\theta_i$ podría representar la probabilidad de supervivencia en cada uno de los centros de investigación).

• El parámetro $\bmath{\phi}$ describe alguna característica relevante de la población ($\bmath{\phi}$ podría representar la probabilidad de supervivencia ``global'' para pacientes que sufren de la afección renal bajo estudio).

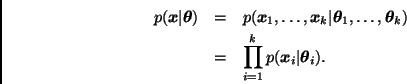
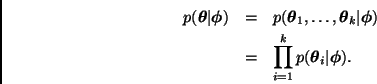
Es claro que estas ideas pueden generalizarse para construir modelos jerárquicos con más de tres niveles. Sin embargo, con el fin de facilitar la exposición, en este trabajo nos concentraremos en modelos de tres niveles.

Covariables

En ocasiones se cuenta con información adicional en forma de covariables $\bmath{z}=(z_1,\ldots,z_r)$, de manera que el conjunto de observaciones está dado por $\{(\bmath{x}_1,\bmath{z}_1),\ldots, (\bmath{x}_k,\bmath{z}_k)\}$. La forma usual de modelar la intercambiabilidad de los parámetros en presencia de covariables es a través del concepto de independencia condicional,

$$p(\bmath{\theta}_1,\ldots,\bmath{\theta}_k\vert\bmath{z}_1,\... ...th{\phi}\vert\bmath{z}_1,\ldots,\bmath{z}_k) \, d\bmath{\phi}.$$

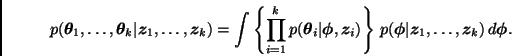
En esencia, esto supone cierta forma de intercambiabilidad parcial (ver Sección 2.2.2).