5 Ejemplo B

Como se mencionó en la Sección 1.2, la función de verosimilitud inducida por una distribución Cauchy puede tener una forma complicada incluso cuando se tienen sólo dos observaciones. Por fortuna, en este caso es posible utilizar el método de variables latentes, aprovechando la representación (4), y obtener así una muestra de la distribución final de $\theta$ a través del algoritmo de Gibbs.

Supongamos que a cada observación $X_1$, $X_2$ se le asocia una variable $\lambda_1$, $\lambda_2$, respectivamente, de tal forma que

$$p(x_1, x_2, \lambda_1, \lambda_2 \vert \theta) = \prod_{i=1}... ...t \theta, 1/\lambda_i) \, \mbox{Ga}(\lambda_i \vert 1/2, 1/2).$$

Entonces

$$p(x_1, x_2 \vert \theta) = \prod_{i=1}^2 p(x_i \vert \theta),$$

es decir, la densidad marginal de $(X_1,X_2)$ corresponde a la del modelo original.

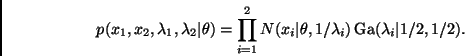
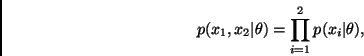
Por otro lado, dado que $p(\theta) \propto 1$ se tiene que

$$p(\theta \vert \lambda_1, \lambda_2, \bmath{x}) = N(\theta \vert \mu_0, \sigma^2_0)$$ (12)

y

$$p(\lambda_1, \lambda_2 \vert \theta, \bmath{x}) = \prod_{i=... ...\mbox{Ga}(\lambda_i \vert 1, \{ 1 + ( \theta - x_i)^2 \} / 2),$$ (13)

donde

$$\mu_0 = \frac{\lambda_1 x_1 + \lambda_2 x_2}{\lambda_1 + \la... ... \ y \ \ \ \ \ } \sigma^2_0 = \frac{1}{\lambda_1 + \lambda_2}.$$

Figure 4: Promedios ergódicos

Figure 5: Distribución final de $\theta$

Las densidades condicionales completas (13) y (14) pueden ahora utilizarse en el muestreo de Gibbs. En este caso se corrió el algoritmo durante 1100 iteraciones, de las cuales se tomaron las primeras 100 como periodo de calentamiento, para generar una muestra de tamaño $N=5000$. La Figura 4 presenta los promedios ergódicos de las medias muestrales de $\theta$, $\lambda_1$ y $\lambda_2$, así como los histogramas correspondientes. En la Figura 5 se muestra el histograma para $\theta$ junto con una estimación de la función de densidad $p(\theta \vert \bmath{x})$. Como era de esperarse, esta densidad es bimodal (con modas en $\theta = -4.876482$ y $\theta = 2.847174$). Por otra parte, $\hat{E}_{MG}(\theta \vert \bmath{x}) = -1.013873$ y $\widehat{\mbox{Var}}_{MG}(\theta \vert \bmath{x}) = 17.321513$, aunque debe señalarse que la información proporcionada por la media y la varianza no es muy relevante en este caso.