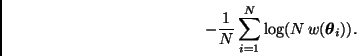Supongamos ahora que
![]() y que se requiere
evaluar la integral
y que se requiere
evaluar la integral
Si ahora generamos una muestra
![]() de
de
![]() entonces podemos aproximar la integral
entonces podemos aproximar la integral ![]() a través
del estimador insesgado
a través
del estimador insesgado

La varianza de este estimador está dada por
La precisión de ![]() depende tanto del tamanõ de muestra,
depende tanto del tamanõ de muestra, ![]() ,
como de la distribución de muestreo por importancia,
,
como de la distribución de muestreo por importancia,
![]() .
De hecho, si
.
De hecho, si
![]() se elige proporcional a
se elige proporcional a
![]() entonces Var
entonces Var
![]() sin importar el tamaño de muestra. Por
supuesto en la práctica dicha elección no es posible, pero esta idea
sugiere que
sin importar el tamaño de muestra. Por
supuesto en la práctica dicha elección no es posible, pero esta idea
sugiere que
![]() debe tener una forma similar a la de
debe tener una forma similar a la de
![]() , excepto tal vez en regiones donde los valores de
, excepto tal vez en regiones donde los valores de
![]() sean despreciables.
sean despreciables.

Tenemos entonces que, para una integral ![]() dada, existe una infinidad de
estimadores insesgados, en principio con precisiones distintas. Un aspecto
importante del método de Monte Carlo se refiere al diseño de técnicas
de reducción de varianza para dichos estimadores. Una de las técnicas
más sencillas consiste precisamente en elegir una distribución de
muestreo por importancia adecuada. Generalmente se requiere que
dada, existe una infinidad de
estimadores insesgados, en principio con precisiones distintas. Un aspecto
importante del método de Monte Carlo se refiere al diseño de técnicas
de reducción de varianza para dichos estimadores. Una de las técnicas
más sencillas consiste precisamente en elegir una distribución de
muestreo por importancia adecuada. Generalmente se requiere que
![]() satisfaga las siguientes condiciones:
satisfaga las siguientes condiciones:
(a) debe ser fácil de simular;
(b) debe tener una forma similar a la de
![]() , la función
que se desea integrar;
, la función
que se desea integrar;
(c) debe tener las colas más pesadas que
![]() , pues de
otra forma la varianza de
, pues de
otra forma la varianza de ![]() podría llegar
a ser muy
grande o incluso infinita.
podría llegar
a ser muy
grande o incluso infinita.
En la práctica es común trabajar en términos de alguna
reparametrización
![]() ,
de manera que la integral esté definida sobre todo
,
de manera que la integral esté definida sobre todo ![]() . Es este caso,
el uso de la distribución
. Es este caso,
el uso de la distribución ![]() de Student (con pocos grados de libertad)
como distribución de muestreo por importancia es bastante frecuente.
de Student (con pocos grados de libertad)
como distribución de muestreo por importancia es bastante frecuente.
Como una aplicación interesante de este método, consideremos el
problema de calcular el valor esperado de una función
![]() respecto a la distribución final
respecto a la distribución final
![]() ,
i.e.
,
i.e.
Sea
![]() una distribución de muestreo por importancia.
Estimando por separado cada una de las integrales en (10) tenemos
una distribución de muestreo por importancia.
Estimando por separado cada una de las integrales en (10) tenemos
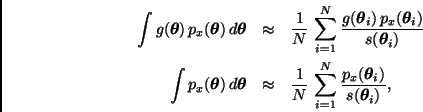
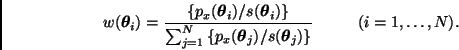
Este estimador es sólo asintóticamente insesgado. En problemas de este
tipo es común elegir
![]() de acuerdo con la forma de
de acuerdo con la forma de
![]() , es decir, de la distribución final, pero con las
colas más pesadas. Si las colas de
, es decir, de la distribución final, pero con las
colas más pesadas. Si las colas de
![]() son más ligeras
que las de
son más ligeras
que las de
![]() entonces
entonces
![]() puede
llegar a ser muy grande, lo cual haría que el estimador (11)
fuera inestable. Por esta razón es conveniente que los pesos sean todos
del mismo orden. De hecho, si
puede
llegar a ser muy grande, lo cual haría que el estimador (11)
fuera inestable. Por esta razón es conveniente que los pesos sean todos
del mismo orden. De hecho, si
![]() entonces
entonces
![]() para toda
para toda ![]() .
.
Lo anterior sugiere una manera de verificar la convergencia del estimador
(11): comparar los pesos
![]() con una
distribución uniforme discreta sobre
con una
distribución uniforme discreta sobre
![]() , digamos a
través de la divergencia logarítmica de Kullback-Leibler, i.e.
, digamos a
través de la divergencia logarítmica de Kullback-Leibler, i.e.