

Next: 2 Muestreo por Importancia
Up: 4 Método de Monte
Previous: 4 Método de Monte
La idea básica del método de Monte Carlo consiste en escribir
la integral requerida como el valor esperado de alguna función
con respecto a alguna distribución de probabilidad, lo cual sugiere
una solución ``estadística'' al problema de integración.
Para motivar la discusión consideremos el siguiente ejemplo.
Sea
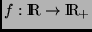 . Supongamos que existe
. Supongamos que existe 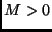 tal que
tal que
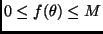 para todo
para todo
![$\theta \in [a,b] \,$](img238.png) y que se desea
calcular la integral
y que se desea
calcular la integral
El valor de esta integral no es más que el área bajo la curva
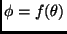 para
para
![$\theta \in [a,b]$](img240.png) . Dicha gráfica queda
inscrita en el rectángulo
. Dicha gráfica queda
inscrita en el rectángulo
![$R = [a,b] \times [0,M]$](img241.png) .
.
Sea
Entonces
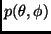 corresponde a la función de densidad
(respecto a la medida de Lebesgue) de una distribución uniforme
sobre el rectángulo
corresponde a la función de densidad
(respecto a la medida de Lebesgue) de una distribución uniforme
sobre el rectángulo  . La integral
. La integral  puede entonces estimarse
simulando una muestra
puede entonces estimarse
simulando una muestra
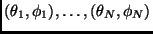 de
de
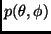 y contando cuántos de estos valores caen bajo la
curva
y contando cuántos de estos valores caen bajo la
curva
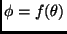 . Específicamente, sea
. Específicamente, sea
donde
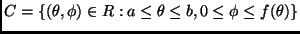 .
Entonces
.
Entonces
es un estimador insesgado de 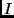 . En efecto, cada observación
. En efecto, cada observación
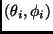 corresponde a un ensayo Bernoulli con probabilidad de
éxito
corresponde a un ensayo Bernoulli con probabilidad de
éxito
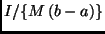 , por lo que
, por lo que
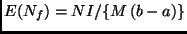 .
Más aún, la varianza de este estimador es
.
Más aún, la varianza de este estimador es
Ripley (1987) discute algunas técnicas de simulación estocástica y
ofrece una introducción básica al método de Monte Carlo.


Next: 2 Muestreo por Importancia
Up: 4 Método de Monte
Previous: 4 Método de Monte
![]() . Supongamos que existe
. Supongamos que existe ![]() tal que
tal que
![]() para todo
para todo
![]() y que se desea
calcular la integral
y que se desea
calcular la integral
