Supongamos por el momento que
![]() y
notemos que
y
notemos que
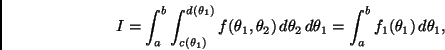
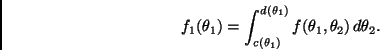
En principio es posible utilizar alguna regla de integración univariada
para integrar ![]() , digamos
, digamos
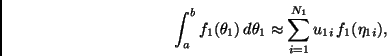
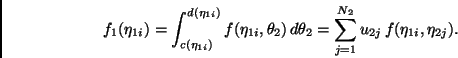
La regla resultante en dos dimensiones está dada entonces por
Podemos pensar ahora en (9) como una sola regla bidimensional con
![]() nodos dados por
nodos dados por
![]() y pesos
asociados
y pesos
asociados
![]() . Las reglas de la forma
(9) son conocidas como reglas cartesianas. La extensión al
caso de
. Las reglas de la forma
(9) son conocidas como reglas cartesianas. La extensión al
caso de ![]() dimensiones es directa. En general las reglas cartesianas
pueden llegar a ser bastante ineficientes, incluso para valores moderados
de
dimensiones es directa. En general las reglas cartesianas
pueden llegar a ser bastante ineficientes, incluso para valores moderados
de ![]() .
.
![]() Cuadratura de Gauss-Hermite. En el caso
multidimensional, los nodos de la regla de Gauss-Hermite corresponden a los
vértices de una retícula cartesiana. Si la correlación entre los
elementos de
Cuadratura de Gauss-Hermite. En el caso
multidimensional, los nodos de la regla de Gauss-Hermite corresponden a los
vértices de una retícula cartesiana. Si la correlación entre los
elementos de
![]() es muy alta entonces muchos de estos nodos
estarán ubicados en zonas donde la densidad toma valores muy pequeños.
En la versión general del método iterativo de Naylor y Smith (1982)
mencionado en la sección anterior, en cada iteración el estimador
de la matriz de varianzas-covarianzas es utilizado para definir la
transformación
es muy alta entonces muchos de estos nodos
estarán ubicados en zonas donde la densidad toma valores muy pequeños.
En la versión general del método iterativo de Naylor y Smith (1982)
mencionado en la sección anterior, en cada iteración el estimador
de la matriz de varianzas-covarianzas es utilizado para definir la
transformación
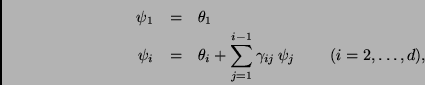
![]() Reglas esféricas. Una alternativa a la regla
cartesiana de Gauss-Hermite consiste en reescribir el problema en términos
de coordenadas esféricas y construir reglas de integración cuyos
nodos estén colocados simétricamente sobre esferas concéntricas.
Estas reglas son bastante eficientes cuando
Reglas esféricas. Una alternativa a la regla
cartesiana de Gauss-Hermite consiste en reescribir el problema en términos
de coordenadas esféricas y construir reglas de integración cuyos
nodos estén colocados simétricamente sobre esferas concéntricas.
Estas reglas son bastante eficientes cuando ![]() , pero para
, pero para
![]() pueden ser inestables.
pueden ser inestables.