2 Cuadratura de Gauss-Hermite

Para facilitar la exposición, por el momento discutiremos solamente el caso univariado, dejando el caso general para la Sección 3.3.

Supongamos que se desea calcular la integral

$$I = \int_{-\infty}^{\infty} f(\theta) \, d \theta.$$

En aplicaciones Bayesianas, dada la normalidad asintótica de la distribución final, tiene sentido suponer que los integrandos que nos interesan son aproximadamente de la forma

$$f(\theta) = q(\theta) \, \exp\{ - \theta^2 \},$$

donde $q(\theta)$ es un polinomio de orden pequeño. La regla de Gauss-Hermite aproxima esta integral a través de

$$\hat{I}_{GH} = \sum_{i=1}^{N} \omega_i \, q(r_i),$$

donde $r_i$ es la $i$-ésima raíz de $H_N(t)$ y

$$\omega_i = \frac{ 2^{n-1} \, N! \, \sqrt{\pi} } { N^2 \, H_{N-1}(r_i)^2 }.$$

Aquí $H_N(t)$ denota al polinomio de Hermite de orden $N$. La Tabla 1 muestra los valores de $\{r_i\}$ y $\{\omega_i\}$ para algunos valores de $N$. Abramowitz y Stegun (1965, p. 924) presentan una tabla más completa que incluye valores hasta para $N=20$.

Table 1: Nodos y pesos para la regla de Gauss-Hermite

N	$\pm r_i$	$\omega_i$
2	0.7071067812	8.8622693 $\times 10^{-1}$
3	0.0000000000	1.1816359
	1.2247448714	2.9540898 $\times 10^{-1}$
4	0.5246476233	8.0491409 $\times 10^{-1}$
	1.6506801239	8.1312835 $\times 10^{-2}$
5	0.0000000000	9.4530872 $\times 10^{-1}$
	0.9585724646	3.9361932 $\times 10^{-1}$
	2.0201828705	1.9953242 $\times 10^{-2}$

Notemos que

$$\hat{I}_{GH} = \sum_{i=1}^{N} \omega_i \, q(r_i) = \sum_{i=1}^{N} u_i \, f(\eta_i),$$

con $\eta_i = r_i$ y $u_i = \omega_i \, \exp\{ r_i^2 \}$.

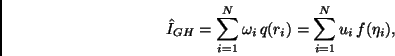
Esta regla elige los nodos y los pesos de manera que la aproximación sea exacta si $q(\theta)$ es un polinomio de orden a lo más $(2N-1)$ en $\theta$. Es posible extender esta técnica para evaluar integrales cuyo integrando es de la forma

$$f^*(\theta) = q(\theta) \, N(\theta \vert \mu, \sigma^2),$$

en cuyo caso

$$\hat{I}_{GH}^* = \pi^{-1/2} \, \sum_{i=1}^{N} \omega_i \, q(\mu + \sqrt{2 \sigma^2} \, r_i)$$ (8)

o, equivalentemente,

$$\hat{I}_{GH}^* = \sum_{i=1}^{N} u_i^* \, f^*(\eta_i^*)$$

con $u_i^* =\sqrt{2 \sigma^2} \, \omega_i \, \exp\{ r_i^2 \}$ y $\eta_i^* = \mu + \sqrt{2 \sigma^2} \, r_i$.

Si $\mu$ y $\sigma^2$ son desconocidos también lo serán los nodos $\{ \eta_i^* \}$. Sin embargo, es posible estimar $\mu$ y $\sigma^2$ iterativamente de la siguiente forma (Naylor y Smith 1982): (i) elegir valores iniciales $\mu_0$ y $\sigma^2_0$; (ii) utilizar (8) con $q(\theta)=\theta$ y $q(\theta)=\theta^2$ para actualizar los valores de $\mu$ y $\sigma^2$, respectivamente;
(iii) repetir el paso anterior hasta que los valores de los estimadores se estabilicen.