4 Inferencia y predicción

Inferencia sobre $\sigma^2$

De acuerdo con los resultados de la sección anterior, la distribución final de $\sigma^2$ es

$$p(\sigma^2\vert\bmath{y}) = IGa(\sigma^2\vert a_1/2,d_1/2).$$

En particular, se tiene que

$$\begin{eqnarray*} E(\sigma^2\vert\bmath{y}) & = & \frac{d_1}{a_1-2} \\ \mbox{Va... ...\\ \mbox{Moda}(\sigma^2\vert\bmath{y}) & = & \frac{d_1}{a_1+2}. \end{eqnarray*}$$

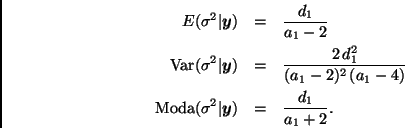
Estas cantidades pueden servir de base para hacer inferencias sobre $\sigma^2$. También es posible construir intervalos de máxima densidad o simplemente reportar algunos percentiles de la distribución final de $\sigma^2$.

Notemos que si se utiliza la distribución de referencia estas expresiones se reducen a

$$\begin{eqnarray*} E(\sigma^2\vert\bmath{y}) & = & \frac{(n-p) \tilde{\sigma}^2}{... ...gma^2\vert\bmath{y}) & = & \frac{(n-p) \tilde{\sigma}^2}{n-p+2}. \end{eqnarray*}$$

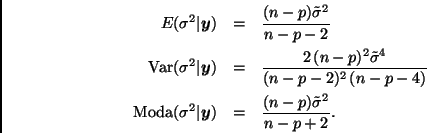
Inferencia sobre $\bmath{\beta}$

La distribución final de $\bmath{\beta}$ está dada por (7). En particular,

$$\begin{array}{cclcl} E(\bmath{\beta}\vert\bmath{y}) & = & \b... ..._1-2)} \, \bmath{B}_1^{-1} & & \mbox{si } a_1 > 2. \end{array}$$

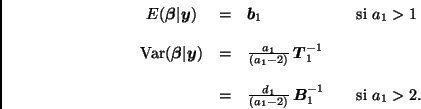
Por otro lado, si se utiliza la distribución de referencia entonces

$$\begin{array}{cclcl} E(\bmath{\beta}\vert\bmath{y}) & = & \h... ...(\bmath{X}'\bmath{X})^{-1} & & \mbox{si } n > p+2. \end{array}$$

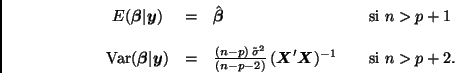
Como en el caso anterior, estas cantidades pueden servir de base para hacer inferencias sobre $\bmath{\beta}$. Notemos, sin embargo, que en este caso el interés se centra generalmente en combinaciones lineales de las entradas del vector $\bmath{\beta}$.

Sea $\bmath{\gamma} = \bmath{C}\bmath{\beta}$, donde $\bmath{C}$ es una matriz $r \times p$ de rango $r \;\, (r \leq p)$. Entonces

$$p(\bmath{\gamma}\vert\sigma^2,\bmath{y}) = N_r(\bmath{\gamma}\vert\bmath{g},\sigma^2 \bmath{G}),$$

donde $\bmath{g}=\bmath{C}\bmath{b}_1$ y $\bmath{G}=\bmath{C}\bmath{B}_1^{-1}\bmath{C}'$. Por lo tanto

$$p(\bmath{\gamma}\vert\bmath{y}) = St_r(\bmath{\gamma}\vert\bmath{g},(d_1/a_1)\bmath{G},a_1).$$

Supongamos, por ejemplo, que $r=1$ y $\bmath{C}=\bmath{e}_i'=(0,\ldots,1,\ldots,0)$ para alguna $i=1,\ldots,p$. Entonces $\gamma=\bmath{e}_i'\bmath{\beta}=\beta_{i-1}$. En este caso $g=\bmath{e}_i'\bmath{b}_1=b_{1,i-1}$ y $G=B_1^{ii}$, donde $B_1^{ii}$ es la entrada $(i,i)$ de la matriz $\bmath{B}_1^{-1}$. Por lo tanto,

$$p(\beta_j\vert\bmath{y})=St(\beta_j\vert b_{1j},(d_1/a_1) B_1^{j+1,j+1},a_1) \;\;\;\;\; (j=0,1,\ldots,k).$$

Predicción

Supongamos que se desea predecir $Y_*$, un nuevo valor de la variable de respuesta, dado el vector de covariables $\bmath{x}_*'=(1,x_{1*},\ldots,x_{k*})$. De acuerdo con el modelo,

$$\begin{eqnarray*} Y_* & = & \beta_0 + \beta_1 x_{1*} + \ldots + \beta_k x_{k*} + \epsilon_*\\ & = & \bmath{x}_*' \bmath{\beta} + \epsilon_*, \end{eqnarray*}$$

donde $\epsilon_* \sim N(0,\sigma^2)$ es independiente de $\bmath{\epsilon}$. Entonces,

$$\mu_* \stackrel{\mbox{\footnotesize def}}{=} E(Y_*\vert\bmath{\beta},\sigma^2) = \bmath{x}_*' \bmath{\beta}$$

y

$$\mbox{Var}(Y_*\vert\bmath{\beta},\sigma^2) = \sigma^2.$$

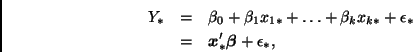
El problema de predicción puede abordarse de dos maneras:

(a) Inferencia sobre $\mu_*$. El parámetro $\mu_*$, que corresponde al valor esperado de la observación futura $Y_*$, no es más que una combinación lineal de los coeficientes de regresión.

Sea $r=1$ y $\bmath{C}=\bmath{x}_*'$. Entonces $\gamma=\bmath{x}_*' \bmath{\beta}=\mu_*$, $g=\bmath{x}_*' \bmath{b}_1$ y $G=\bmath{x}_*' \bmath{B}_1^{-1}\bmath{x}_*$, por lo que

$$p(\mu_*\vert\bmath{y}) = St(\mu_*\vert\bmath{x}_*' \bmath{b}_1, (d_1/a_1) \bmath{x}_*' \bmath{B}_1^{-1}\bmath{x}_*, a_1).$$

En particular, si se utiliza la distribución de referencia entonces

$$\pi(\mu_*\vert\bmath{y}) = St(\mu_*\vert\bmath{x}_*' \hat{\b... ...a}^2 \bmath{x}_*' (\bmath{X}'\bmath{X})^{-1}\bmath{x}_*, n-p).$$

En este caso, el intervalo de máxima densidad del $(1-\alpha) \times 100\%$ está dado por

$$\bmath{x}_*' \hat{\bmath{\beta}} \pm t_{(n-p)}^{1-\alpha/2} ... ...a} \sqrt{\bmath{x}_*' (\bmath{X}'\bmath{X})^{-1}\bmath{x}_*},$$

donde $t_{(n-p)}^{1-\alpha/2}$ es el cuantil de orden $(1-\alpha/2)$ de una distribución $t$ de Student estandarizada con $(n-p)$ grados de libertad. Este intervalo tiene la misma forma que el correspondiente intervalo frecuentista.

(b) Inferencia sobre $Y_*$. En este caso interesa calcular la distribución predictiva final para $Y_*$,

$$p(y_*\vert\bmath{y}) = \int \int p(y_*\vert\bmath{\beta},\s... ...\beta},\sigma^2\vert\bmath{y}) \, d\bmath{\beta} \, d\sigma^2.$$

Recordemos primero que $Y_*=\bmath{x}_*' \bmath{\beta}+\epsilon_*$. Trabajando condicionalmente en $\sigma^2$, tenemos que $\bmath{\beta}$ y $\epsilon_*$ son independientes y

$$\begin{eqnarray*} p(\bmath{\beta}\vert\sigma^2,\bmath{y}) & = & N_p(\bmath{\bet... ...lon_*\vert\sigma^2,\bmath{y}) & = & N(\epsilon_*\vert,\sigma^2). \end{eqnarray*}$$

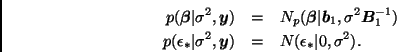
Esto implica que

$$p(y_*\vert\sigma^2,\bmath{y}) = N(y_*\vert\bmath{x}_*' \bma... ... \sigma^2 \{ 1 + \bmath{x}_*' \bmath{B}_1^{-1} \bmath{x}_*\}).$$

Finalmente, integrando con respecto a la distribución final de $\sigma^2$,

$$p(y_*\vert\bmath{y}) = St(y_*\vert\bmath{x}_*' \bmath{b}_1, ... .../a_1) \{ 1 + \bmath{x}_*' \bmath{B}_1^{-1} \bmath{x}_*\},a_1).$$

Si se utiliza la distribución de referencia entonces la distribución predictiva final toma la forma

$$p(y_*\vert\bmath{y}) = St(y_*\vert\bmath{x}_*' \hat{\bmath{\... ...+ \bmath{x}_*' (\bmath{X}'\bmath{X})^{-1}\bmath{x}_* \}, n-p).$$

En este caso, el intervalo de máxima densidad del $(1-\alpha) \times 100\%$ está dado por

$$\bmath{x}_*' \hat{\bmath{\beta}} \pm t_{(n-p)}^{1-\alpha/2} ... ...\sqrt{1 + \bmath{x}_*' (\bmath{X}'\bmath{X})^{-1}\bmath{x}_*}.$$

Como en el caso anterior, este intervalo tiene la misma forma que el correspondiente intervalo frecuentista.