3 Distribución final

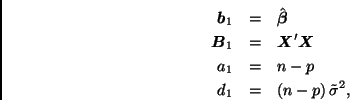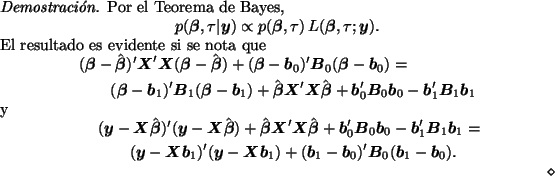
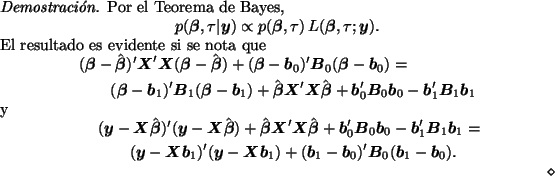
De acuerdo con este resultado, la distribución marginal final de $\tau$ es

$$p(\tau\vert\bmath{y}) = Ga(\tau\vert a_1/2,d_1/2),$$

lo que implica que la correspondiente distribución final para $\sigma^2$ es $IGa(\sigma^2\vert a_1/2,d_1/2)$.

Por otro lado, si se desea hacer inferencias sobre $\bmath{\beta}$ entonces es necesario calcular su distribución marginal final, dada por

$$\begin{eqnarray*} p(\bmath{\beta}\vert\bmath{y}) & = & \int p(\bmath{\beta},\ta... ...'\bmath{B}_1 (\bmath{\beta}-\bmath{b}_1) \right\}^{-(a_1+p)/2}. \end{eqnarray*}$$

En otras palabras,

$$p(\bmath{\beta}\vert\bmath{y}) = St_p(\bmath{\beta}\vert\bmath{b}_1,\bmath{T}_1^{-1},a_1),$$ (5)

donde $\bmath{T}_1 = \left(\frac{a_1}{d_1}\right) \bmath{B}_1$, de manera que la distribución final de $\bmath{\beta}$ es $t$ de Student con $a_1$ grados de libertad, parámetro de localización $\bmath{b}_1$, y parámetro de escala $\bmath{T}_1^{-1}$.

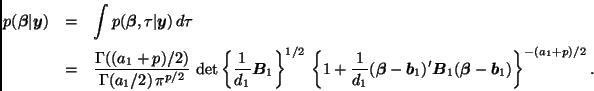
Distribución final de referencia

Recordemos que la distribución inicial de referencia, $\pi(\bmath{\beta},\tau) \propto \tau^{-1}$, corresponde a un caso límite de la familia conjugada (6) con $\bmath{B}_0=\bmath{O}$, $a = -p$ y $d=0$. Aunque es impropia, ésta da lugar a una distribución final propia siempre y cuando $n>p$. De hecho, en este caso se tiene que

$$\begin{eqnarray*} \bmath{b}_1 & = & \hat{\bmath{\beta}} \\ \bmath{B}_1 & = & \b... ...th{X} \\ a_1 & = & n-p \\ d_1 & = & (n-p) \, \tilde{\sigma}^2, \end{eqnarray*}$$

donde $\tilde{\sigma}^2$ es el estimador insesgado usual para $\sigma^2$. Por lo tanto,

$$\pi(\bmath{\beta},\tau\vert\bmath{y}) = N_p(\bmath{\beta}\v... ...h{X})^{-1}) \: Ga(\tau\vert(n-p)/2, (n-p)\tilde{\sigma}^2/2),$$

de donde

$$\pi(\bmath{\beta}\vert\bmath{y}) = St_p(\bmath{\beta}\vert \... ...bmath{\beta}},\tilde{\sigma}^2(\bmath{X}'\bmath{X})^{-1},n-p).$$