Abstract:
In the first part of this talk, following the ideas given by Deheuvels for the empirical copula, we first assume that we are sampling from the product copula, and we construct
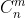
the
d-sample copula of order
m. Then we study the distribution of the number of observations in each of the boxes generated by the regular partition of order
m in
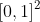
, and then we give the associated moments and correlations. We also give generalizations of these results for the
d-dimensional case, when
d > 2.
In the second part, we study the weak convergence of the sample process, that is,
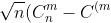}))
, where
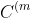})
is the checkerboard approximation of order of the real copula
C, see Li
et al. when the partial derivatives of
C are continuous, with or without the independence assumption. In this way we will have, for the sample copula, a weak convergence theorem similar to that for the empirical copula. In order to apply the results of weak convergence for the empirical process, we show that the sample copula can be represented as a linear functional of the empirical copula, and then we can apply the delta method. Finally, we perform several simulations of the sample process at a given point to find an adequate sample size that provides the convergence to a centered Gaussian process with a given variance-covariance structure.