1 Aproximación normal asintótica

Para facilitar la exposición nos concentraremos en el caso univariado ($d=1$). El caso multivariado es completamente análogo.

Sea $p_x(\theta) = p(\theta) \, p(\bmath{x} \vert \theta)$ y denotemos por $\hat{\theta}$ a la moda de $p_x(\theta)$. Desarrollando $\log p_x(\theta)$ en serie de Taylor alrededor de $\hat{\theta}$ tenemos

$$\log p_x(\theta) = \log p_x(\hat{\theta}) + \sum_{k=1}^\inft... ...hat{\theta})}{\partial \theta^k} \, (\theta - \hat{\theta})^k.$$

Más adelante veremos que las aproximaciones se requieren principalmente en regiones tales que $(\theta - \hat{\theta})$ es de orden $O(n^{-1/2})$, por lo que en la discusión siguiente supondremos que

$$(\theta - \hat{\theta}) = O(n^{-1/2}) \; \; \; \; \; \; \; (n \rightarrow \infty).$$

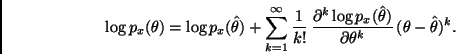
Por otra parte, notemos que

$$\log p_x(\theta) = \log p(\theta) + \sum_{i=1}^n \log p(x_i \vert \theta),$$

de donde

$$\begin{eqnarray*} \frac{\partial^k \log p_x(\theta)}{\partial \theta^k} & = & \f... ...l \theta^k} \\ & = & O(n) \mbox{\ \ \ para toda } k=1,2,\ldots \end{eqnarray*}$$

Así,

$$\frac{1}{k!} \frac{\partial^k \log p_x(\hat{\theta})}{\parti... ...\theta})^k = O(n^{1-k/2}) \mbox{\ \ \ para toda } k=1,2,\ldots$$

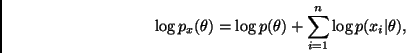
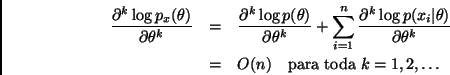
Ahora, sea

$$V(\theta) = - \left\{ \frac{\partial^2 \log p_x(\theta)}{\partial \theta^2} \right\}^{-1}$$

y notemos que

$$\frac{\partial \log p_x(\hat{\theta})}{\partial \theta} = 0.$$

Entonces

$$\log p_x(\theta) = \log p_x(\hat{\theta}) - \frac{1}{2 \, V(\hat{\theta})} (\theta - \hat{\theta})^2 + O(n^{-1/2}),$$

y por lo tanto

$$p_x(\theta) = p_x(\hat{\theta}) \, \exp \left\{ - \frac{1}{2... ...)}(\theta - \hat{\theta})^2 \right\} \, \{ 1 + O(n^{-1/2}) \}.$$

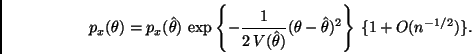
Por otro lado, como consecuencia del Corolario 2.1 tenemos que

$$\int p_x(\theta) \, d\theta = p_x(\hat{\theta}) \, (2 \pi)^{1/2} \, V(\hat{\theta})^{1/2} \, \{ 1 + O(n^{-1}) \},$$

de donde

$$p(\theta \vert \bmath{x}) = (2 \pi)^{-1/2} \, V(\hat{\theta}... ...)}(\theta - \hat{\theta})^2 \right\} \, \{ 1 + O(n^{-1/2}) \}.$$

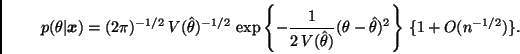
Comentario. Recordemos que $V(\theta) = O(n^{-1})$. Tenemos entonces que la desviación estándar asintótica, $\sqrt{V(\theta)}$, es de orden $O(n^{-1/2})$. Así, las aproximaciones se requieren solamente en regiones tales que $(\theta - \hat{\theta})$ es de orden $O(n^{-1/2})$, puesto que fuera de estas regiones $p(\theta \vert \bmath{x})$ es (asintóticamente) muy pequeña.

En el caso multiparametral, un argumento análogo permite demostrar la siguiente versión de la aproximación normal asintótica a la distribución final de $\bmath{\theta}$.

Si esta aproximación es adecuada, entonces prácticamente cualquier resumen inferencial de interés (e.g. distribuciones marginales o momentos de funciones lineales de $\bmath{\theta}$) puede aproximarse fácilmente. En particular,

$$E(\bmath{\theta} \vert \bmath{x}) = \hat{\bmath{\theta}} \: ... ...{x}) = \bmath{V}(\hat{\bmath{\theta}}) \: \{ 1 + O(n^{-1}) \}.$$

Desafortunadamente, en aplicaciones específicas no siempre es fácil determinar si la aproximación normal es adecuada para el tamaño de muestra dado.