Al igual que el algoritmo de Metropolis, el algoritmo de Gibbs
permite simular una cadena de Markov
![]() con distribución de
equilibrio
con distribución de
equilibrio
![]() . En este caso, sin embargo, cada
nuevo valor de la cadena se obtiene a través de un proceso iterativo que
sólo requiere generar muestras de distribuciones cuya dimensión es menor
que
. En este caso, sin embargo, cada
nuevo valor de la cadena se obtiene a través de un proceso iterativo que
sólo requiere generar muestras de distribuciones cuya dimensión es menor
que ![]() y que en la mayoría de los casos tienen una forma más
sencilla que la de
y que en la mayoría de los casos tienen una forma más
sencilla que la de
![]() .
.
Sea
![]() una
partición del vector
una
partición del vector
![]() , donde
, donde
![]() y
y
![]() . Las densidades
. Las densidades
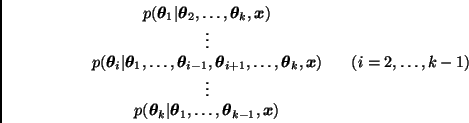
Dado un valor inicial
![]() , el algoritmo
de Gibbs simula una cadena de Markov en la que
, el algoritmo
de Gibbs simula una cadena de Markov en la que
![]() se obtiene a partir de
se obtiene a partir de
![]() de la siguiente manera:
de la siguiente manera:
generar una observación
![]() de
de
![]() ;
;
generar una observación
![]() de
de
![]() ;
;
![]()
generar una observación
![]() de
de
![]() .
.
La sucesión
![]() así
obtenida es entonces una realización de una cadena de Markov cuya
distribución de transición está dada por
así
obtenida es entonces una realización de una cadena de Markov cuya
distribución de transición está dada por
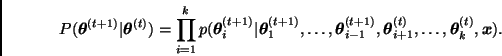
Comentario. En ocasiones la distribución final implica cierta
estructura de independencia condicional entre algunos de los elementos
del vector
![]() . Es estos casos es común que muchas de las
densidades condicionales completas se simplifiquen.
. Es estos casos es común que muchas de las
densidades condicionales completas se simplifiquen.
El siguiente ejemplo presenta una aplicación interesante del muestreo de Gibbs al problema de observaciones faltantes.