Los métodos de integración numérica, también conocidos
como métodos de cuadratura, permiten calcular eficientemente algunas
características de la distribución final de
![]() cuando la dimensión de éste es pequeña.
cuando la dimensión de éste es pequeña.
Sea
![]() una función suave y supongamos que se
desea calcular la integral
una función suave y supongamos que se
desea calcular la integral

A continuación describiremos dos de las reglas más sencillas
utilizadas comúnmente en la práctica. Por el momento nos concentraremos
en el caso univariado, en el cual interesa evaluar integrales de la forma
Sean
![]() los valores de
los valores de
![]() puntos distribuidos sobre el intervalo
puntos distribuidos sobre el intervalo ![]() . En particular,
si los puntos son equidistantes entonces
. En particular,
si los puntos son equidistantes entonces
![]() Regla del punto medio. Está dada por
Regla del punto medio. Está dada por
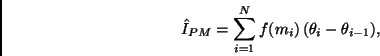
Si los nodos son equidistantes entonces
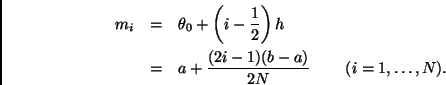
Por lo tanto
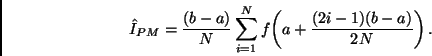
![]() Regla trapezoidal. Esta regla está definida por
Regla trapezoidal. Esta regla está definida por
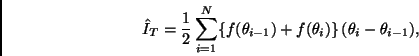
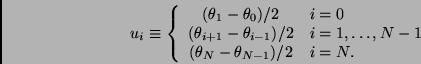
Si los nodos son equidistantes entonces
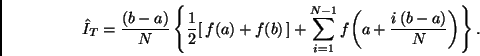
Comentario. En algunas aplicaciones se requiere integrar sobre
regiones no acotadas tales como
![]() ó
ó ![]() ,
en cuyo caso las reglas descritas anteriormente no pueden aplicarse
directamente. Una alternativa consiste en elegir límites
,
en cuyo caso las reglas descritas anteriormente no pueden aplicarse
directamente. Una alternativa consiste en elegir límites ![]() y
y ![]()
![]() de manera que el valor de
de manera que el valor de ![]() sea despreciable fuera del
intervalo
sea despreciable fuera del
intervalo ![]() . Como otra posibilidad, notemos que a través de un
cambio de variable apropiado la integral requerida puede reescribirse
como
. Como otra posibilidad, notemos que a través de un
cambio de variable apropiado la integral requerida puede reescribirse
como

La regla de integración discutida en la siguiente sección permite
calcular de manera exacta la integral de ciertas funciones definidas
sobre todo ![]() y produce buenas aproximaciones para una clase muy
amplia de funciones.
y produce buenas aproximaciones para una clase muy
amplia de funciones.