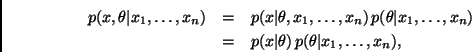![[*]](footnote.png) ,
,
Sea
![]() una muestra aleatoria de una distribución desconocida
una muestra aleatoria de una distribución desconocida
![]() . En Estadística es común considerar una familia paramétrica
de densidades
. En Estadística es común considerar una familia paramétrica
de densidades![[*]](footnote.png) ,
,
En muchas ocasiones el propósito de un análisis estadístico es
predecir el valor de una observación futura ![]() con base en la
información disponible. Ahora bien, el problema de inferencia sobre
con base en la
información disponible. Ahora bien, el problema de inferencia sobre
![]() puede considerarse como un paso intermedio en la solución al
problema de predicción, aunque en ciertas situaciones puede ser de
interés en sí mismo. Por otro lado, debido a resultados de
consistencia, un parámetro puede verse como el límite de una
sucesión de estadísticas (funciones de las observaciones)
cuando el tamaño de muestra tiende a infinito. De esta manera, hacer
inferencias acerca del valor del parámetro
puede considerarse como un paso intermedio en la solución al
problema de predicción, aunque en ciertas situaciones puede ser de
interés en sí mismo. Por otro lado, debido a resultados de
consistencia, un parámetro puede verse como el límite de una
sucesión de estadísticas (funciones de las observaciones)
cuando el tamaño de muestra tiende a infinito. De esta manera, hacer
inferencias acerca del valor del parámetro ![]() puede considerarse
como una forma límite de hacer inferencias predictivas acerca de las
observaciones. Esto será discutido con más detalle en la
Sección 2.3.
puede considerarse
como una forma límite de hacer inferencias predictivas acerca de las
observaciones. Esto será discutido con más detalle en la
Sección 2.3.
Dado el valor de ![]() , la distribución que describe el comportamiento
de la observación futura
, la distribución que describe el comportamiento
de la observación futura ![]() es
es ![]() . Sin embargo, el valor de
. Sin embargo, el valor de
![]() es desconocido. Los métodos estadísticos tradicionales atacan
este problema estimando a
es desconocido. Los métodos estadísticos tradicionales atacan
este problema estimando a ![]() con base en la muestra observada,
y en muchos casos simplemente sustituyen el valor de
con base en la muestra observada,
y en muchos casos simplemente sustituyen el valor de ![]() con
la estimación resultante.
con
la estimación resultante.
Desde la perspectiva Bayesiana, el modelo ![]() , junto con la
distribución inicial
, junto con la
distribución inicial ![]() , induce una distribución conjunta para
, induce una distribución conjunta para
![]() , dada por
, dada por
De manera similar, una vez obtenida la muestra, el modelo ![]() y la
distribución final inducen una distribución conjunta para
y la
distribución final inducen una distribución conjunta para ![]() condicional en los valores observados
condicional en los valores observados
![]() ;
;