1 Muestreo-remuestreo

Supongamos que se tiene una densidad $s(\bmath{\theta})$ de la cual es posible simular observaciones fácilmente, pero que se requiere una muestra de la densidad

$$f(\bmath{\theta}) = \frac{f_0(\bmath{\theta})}{\int f_0(\bmath{\theta}') \, d \bmath{\theta}'},$$

donde sólo la forma funcional de $f_0(\bmath{\theta})$ está especificada. El problema es entonces obtener una muestra de $f(\bmath{\theta})$ a partir de $f_0(\bmath{\theta})$ y de una muestra de $s(\bmath{\theta})$.

$\diamond$ Caso 1. Si existe una constante $M>0$ tal que $f_0(\bmath{\theta}) / s(\bmath{\theta}) \leq M$ para todo $\bmath{\theta}$, entonces es posible utilizar el método de aceptación y rechazo para generar variables aleatorias (ver Ripley 1987). El algoritmo es el siguiente:

1. generar una observación $\tilde{\bmath{\theta}}$ de $s(\bmath{\theta})$;

2. generar una variable $u \sim U(0,1)$;

3. si $u \leq f_0(\tilde{\bmath{\theta}}) / \{ M s(\tilde{\bmath{\theta}}) \}$, aceptar $\tilde{\bmath{\theta}}$ como una observación de $f(\bmath{\theta})$; en caso contrario, repetir los pasos 1 a 3.

Cabe señalar que, dada una muestra de tamaño $N$ de $s(\bmath{\theta})$, el valor esperado para el tamaño de la correspondiente muestra de $f(\bmath{\theta})$ es

$$N_0 = \frac{N}{M} \, \int f_0(\bmath{\theta}) \, d \bmath{\theta}.$$

$\diamond$ Caso 2. Si no existe la cota del punto anterior, o ésta no puede encontrarse fácilmente, entonces podemos obtener muestras aproximadas de $f(\bmath{\theta})$ de la siguiente manera. Supongamos que $\bmath{\theta}_1,\ldots,\bmath{\theta}_N$ es una muestra de $s(\bmath{\theta})$. Sea

$$w_i = \frac{v_i}{\sum_{j=1}^N v_j},$$

donde $v_i = f_0(\bmath{\theta}_i) / s(\bmath{\theta}_i)$, $i=1,\ldots,N$. Lo anterior induce una distribución discreta sobre $\{ \bmath{\theta}_1,\ldots,\bmath{\theta}_N \}$ tal que Pr $(\bmath{\theta} = \bmath{\theta}_i) = w_i$. Si ahora generamos una observación $\tilde{\bmath{\theta}}$ de dicha distribución entonces $\tilde{\bmath{\theta}}$ se distribuye aproximadamente como $f(\bmath{\theta})$. La aproximación es mejor a medida que $N \rightarrow \infty$. Es interesante notar que los pesos $\{ w_i \}$ tienen una forma análoga a los utilizados en el cálculo del estimador $(\ref{eve})$.

A diferencia del caso anterior, aquí es posible muestrear con remplazo, por lo que la muestra generada puede ser tan grande como se quiera. Es claro, sin embargo, que la aproximación será más adecuada a medida que $s(\bmath{\theta})$ se parezca más a $f(\bmath{\theta})$.

Comentario. Existe una dualidad muy interesante entre una muestra dada y la distribución que la genera. Por un lado, la distribución permite generar la muestra; por otro lado, dada la muestra en principio es posible recrear la distribución que la generó (al menos aproximadamente). Este argumento, junto con los métodos discutidos en esta sección, sugiere una versión ``muestral'' del teorema de Bayes al identificar a $s(\bmath{\theta})$ y $f(\bmath{\theta})$ con $p(\bmath{\theta})$ y $p(\bmath{\theta} \vert \bmath{x})$, respectivamente, de manera que $f_0(\bmath{\theta}) = p_x(\bmath{\theta}) = p(\bmath{\theta}) \, p(\bmath{x} \vert \bmath{\theta})$.

$\bullet$ Si existe el estimador de máxima verosimilitud, $\hat{\bmath{\theta}}$, entonces podemos tomar $M = p(\bmath{x} \vert \hat{\bmath{\theta}})$. Es este caso el teorema de Bayes toma una forma muy sencilla: una observación $\tilde{\bmath{\theta}}$ en la muestra de la distribución inicial $p(\bmath{\theta})$ es aceptada como una observación de la distribución final $p(\bmath{\theta} \vert \bmath{x})$ con probabilidad

$$\frac{ f_0(\tilde{\bmath{\theta}}) }{ M \, s(\tilde{\bmath{\... ...bmath{\theta}}) } { p(\bmath{x} \vert \hat{\bmath{\theta}}) }.$$

$\bullet$ Si la cota $M$ no está disponible, dada una muestra $\{ \bmath{\theta}_1,\ldots,\bmath{\theta}_N \}$ de la distribución inicial $p(\bmath{\theta})$ podemos remuestrear observaciones $\tilde{\bmath{\theta}}$ de acuerdo con la distribución discreta

$$\mbox{Pr}(\bmath{\theta} = \tilde{\bmath{\theta}}) = \frac{... ...eta}}) } { \sum_{j=1}^N p(\bmath{x} \vert \bmath{\theta}_j) }.$$

Dichas observaciones se distribuirán entonces aproximadamente como $p(\bmath{\theta} \vert \bmath{x})$. El lector interesado puede consultar el artículo de Smith y Gelfand (1992).

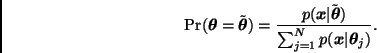
En ambos casos los valores de $\bmath{\theta}$ cuya verosimilitud es alta tienen una mayor probabilidad de quedar representados en la muestra de la distribución final.