1 Introducción

En el enfoque Bayesiano de la Estadística, la incertidumbre presente en un modelo dado, $p(x \vert \bmath{\theta})$, es representada a través de una distribución de probabilidad $p(\bmath{\theta})$ sobre los posibles valores del parámetro desconocido $\bmath{\theta}$ (típicamente multidimensional) que define al modelo. El Teorema de Bayes,

$$p(\bmath{\theta} \vert \bmath{x}) = \frac{p(\bmath{\theta}) \, p(\bmath{x} \vert \bmath{\theta})}{p(\bmath{x})},$$

permite entonces incorporar la información contenida en un conjunto de datos $\bmath{x}=(x_1,\ldots,x_n)$, produciendo una descripción conjunta de la incertidumbre sobre los valores de los parámetros del modelo a través de la distribución final $p(\bmath{\theta} \vert \bmath{x})$. Desafortunadamente, la implementación de las técnicas Bayesianas usualmente requiere de un esfuerzo computacional muy alto. La mayor parte de este esfuerzo se concentra en el cálculo de ciertas características de la distribución final del parámetro de interés (que llamaremos resúmenes inferenciales). Así, por ejemplo, para pasar de una distribución conjunta a una colección de distribuciones y momentos marginales que sean útiles para hacer inferencias sobre subconjuntos de parámetros, se requiere integrar. En la mayoría de los casos los resúmenes inferenciales básicos se reducen a integrales de la forma

$$S_I\{ g(\bmath{\theta}) \} = \int g(\bmath{\theta}) \, p(\bm... ..., p(\bmath{x} \vert \bmath{\theta}) \, d \bmath{\theta}_{I^c},$$

donde $g:\Rex^d \rightarrow \Rex$, $\bmath{\theta}=(\theta_1,\ldots,\theta_d)$, $I \subseteq \{1,\ldots,d \}$, $I^c = \{1,\ldots,d \} \backslash I$ y $\bmath{\theta}_{I^c} = \{ \theta_i : i \in I^c \}$.
Así, por ejemplo,

$$\begin{eqnarray*} p(\bmath{x}) & = & S_\emptyset\{ 1 \}; \\ E(\theta_i \theta_j... ..._\emptyset\{ p(x_F \vert\bmath{\theta}) \} / S_\emptyset\{ 1 \}, \end{eqnarray*}$$

donde $\Ind_A(\cdot)$ denota a la función indicadora del conjunto $A$ y $p(x_F \vert\bmath{x})$ denota a la distribución predictiva de una observación futura $X_F$.

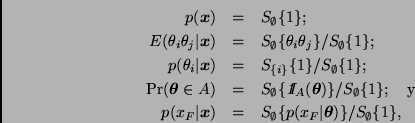
En la práctica es común que la dimensión de $\bmath{\theta}$ sea muy grande. Por otro lado, excepto en aplicaciones muy sencillas tanto $p(\bmath{x} \vert \bmath{\theta})$ como $p(\bmath{\theta})$ pueden llegar a tener formas muy complicadas. En la gran mayoría de los problemas las integrales requeridas no pueden resolverse analíticamente, por lo que es necesario contar con métodos numéricos eficientes que permitan calcular o aproximar integrales en varias dimensiones.

El propósito de estas notas es revisar de manera general algunos de los métodos clásicos para calcular integrales, tales como la aproximación de Laplace, cuadratura (integración numérica) y el método de Monte Carlo, así como discutir algunas de las técnicas de integración desarrolladas durante los últimos años y conocidas con el nombre genérico de técnicas de Monte Carlo vía cadenas de Markov. El lector interesado en el enfoque Bayesiano de la Estadística o en aspectos específicos de los métodos aquí discutidos puede consultar los libros de Bernardo y Smith (1994) y O'Hagan (1994), así como las referencias que ahí se incluyen.

En términos generales, los métodos antes mencionados serán más eficientes y darán resultados más precisos en la medida en que la distribución final sea más parecida a una distribución normal. Es por esta razón que en la mayoría de los casos resulta conveniente trabajar en términos de una reparametrización del modelo, de manera que cada uno de los nuevos parámetros tome valores en todo $\Rex$ y su distribución final sea aproximadamente normal. También es importante que la correlación final entre los nuevos parámetros no sea muy alta.

En lo que resta de esta sección describiremos dos problemas que nos servirán para ilustrar y comparar los métodos discutidos en estas notas. Algunos de estos métodos han sido instrumentados en el lenguaje S de S-Plus. El código correspondiente, así como los resultados principales, pueden encontrarse en los apéndices al final de este trabajo.